Do you know what the mystery of prime factors is? What are the smallest, indivisible building blocks of prime factors? How can you break down any number into its smallest, indivisible building blocks? In this article, we’ll dive into that mystery.
The goal of this article is to provide a comprehensive guide on how to master the art of finding prime factors. Our students will always get a lot of pleasure from studying numbers, regardless of whether they are math enthusiasts, preparing for exams, or simply curious. The goal of our course is to demonstrate various methods, strategies, and real-world applications of prime factorization in an entertaining, educational, and hands-on manner.
If you have fastened your seatbelt, you’ll be able to read the mysteries of prime factors. In the end of this article, you will not only learn how to find prime factors, but you will also appreciate their significance in a variety of life situations. The first thing you should do is dive in.
What Are Prime Factors
When delving into the captivating realm of mathematics, one cannot escape the enigmatic allure of prime factors. So, let’s decipher this mathematical puzzle and grasp the profound significance of prime factors.
Prime factors, simply put, are the elemental building blocks of numbers, the indivisible entities that make up every integer in the universe. They are those unique and unbreakable components that, when multiplied together, form a number. For instance, the number 12 can be expressed as the product of its prime factors, 2 and 3, because 2 * 3 = 12. Prime factors are prime numbers—those integers greater than 1 that have only two distinct divisors, 1 and themselves. These prime numbers, such as 2, 3, 5, 7, 11, and so on, serve as the fundamental elements upon which all other numbers rely for their existence.
Now, you might wonder, “Why should I care about prime factors?” Well, the significance of prime factors extends far beyond the realm of abstract mathematics. Let’s delve into why they matter:
1. Fundamental Theorem of Arithmetic: The understanding of prime factors forms the cornerstone of the Fundamental Theorem of Arithmetic. This theorem asserts that every positive integer greater than 1 can be represented uniquely as a product of prime numbers. In simpler terms, every number has its own secret code—a unique combination of prime factors. This fact is not only mathematically intriguing but also practically useful.
2. Simplifying Fractions: Prime factors play a pivotal role in simplifying fractions. When you know the prime factors of the numerator and denominator, you can cancel out common factors, leading to reduced, more manageable fractions. This is not just a handy trick for math students but also a crucial skill in everyday life when you need to divide and conquer measurements or recipes.
3. Number Properties: Prime factors help us understand the properties of numbers. For instance, knowing the prime factors of a number can reveal whether it’s even or odd. If the number has 2 as one of its prime factors, it’s even; otherwise, it’s odd. Additionally, prime factors can shed light on the divisibility of numbers. If two numbers share the same prime factors, they are divisible by each other.
4. Cryptography: In the world of data security and cryptography, prime factors are more than just mathematical curiosities—they are the linchpin of encryption systems. Prime factorization of large numbers is an incredibly time-consuming task for classical computers, making it the basis for secure encryption algorithms. The difficulty of factoring large semiprime numbers (the product of two prime numbers) underpins the security of online transactions, ensuring your sensitive information remains confidential.
5. Puzzle Solving: Prime factors often make appearances in various puzzles, brainteasers, and competitive exams. They challenge your problem-solving skills and logic, providing an enjoyable mental exercise.
In essence, prime factors are not mere abstractions; they are the hidden architects of the mathematical universe, providing structure, insight, and practical utility. So, whether you’re a student navigating the intricacies of mathematics, a professional in need of fraction simplification skills, or someone simply intrigued by the beauty of numbers, a solid grasp of prime factors is an invaluable asset. It’s a key that unlocks the door to a deeper understanding of math’s underlying principles and opens up a world of practical applications. So, next time you encounter a number, remember that it holds a secret code of prime factors, waiting to be deciphered and appreciated for its mathematical elegance and real-world relevance.
Why Finding Prime Factors Is Useful
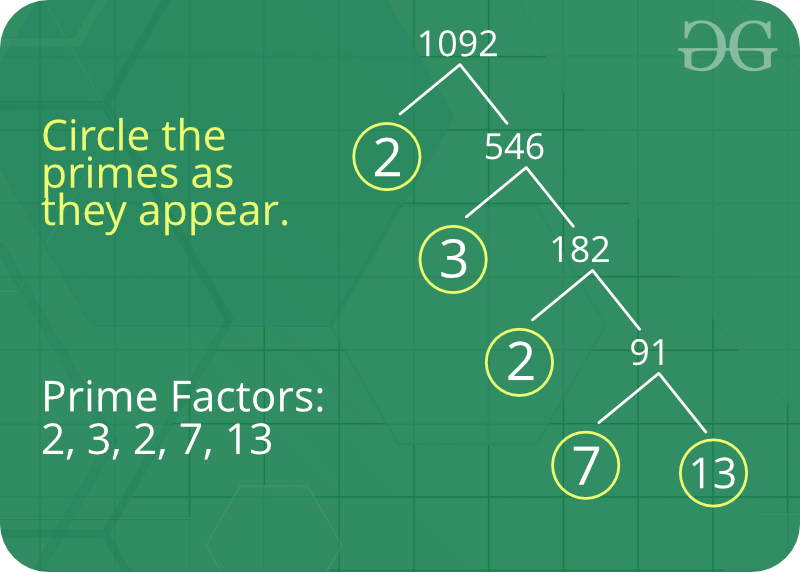
When we dive into the fascinating realm of prime factors, we soon realize that they are not just abstract mathematical entities confined to the pages of textbooks; they have a profound and practical impact on our lives. Let’s explore why finding prime factors is not only useful but also essential in both the world of mathematics and beyond.
Practical Applications of Prime Factorization:
Fraction Simplification: One of the most immediate and practical applications of prime factorization is in the simplification of fractions. Whether you’re a student working on math problems or an everyday person trying to adjust a recipe, prime factors come to your rescue. By breaking down the numerator and denominator of a fraction into their prime factors, you can easily cancel out common factors, simplifying the fraction to its lowest terms. This simplification process is fundamental in various fields, including engineering and science.
Divisibility Testing: Prime factors also play a crucial role in determining the divisibility of numbers. If two numbers share the same prime factors, they are divisible by each other. This knowledge is not just handy for math enthusiasts but also for professionals in fields like finance, where divisibility plays a role in calculating interest rates and payments.
Computer Algorithms: In the digital age, prime factorization takes on a new dimension of significance. It forms the foundation of encryption algorithms, such as RSA, used to secure online transactions, communications, and data storage. The difficulty of factoring large semiprime numbers (the product of two prime numbers) is what makes these encryption systems robust and secure. Without prime factorization, our digital world would be much more vulnerable to security breaches.
Data Compression: In the realm of data storage and transmission, prime factors have a practical application in data compression techniques. For instance, the JPEG image compression algorithm utilizes prime factorization to reduce the size of image files without compromising significant visual quality. This technology is omnipresent in our daily lives, as it allows us to store and share vast amounts of visual data efficiently.
Emphasizing Relevance in Mathematics and Beyond:
Beyond these practical applications, prime factors hold a special place in the field of mathematics itself:
Number Theory: Prime factorization is a fundamental concept in number theory, a branch of mathematics that explores the properties and relationships of integers. Understanding prime factors helps mathematicians tackle some of the most profound and unsolved problems in mathematics, such as the Riemann Hypothesis and the Goldbach Conjecture.
Mathematical Puzzles: Prime factors often make appearances in mathematical puzzles and contests, challenging the minds of mathematicians of all ages. They inspire curiosity, foster problem-solving skills, and fuel a love for mathematics.
Historical Significance: Prime factors have historical significance, dating back to ancient civilizations like the Greeks and Egyptians. They have been instrumental in the development of mathematical thought throughout history.
In conclusion, the importance of prime factors extends far beyond mathematical theory. Their practical applications in simplifying fractions, determining divisibility, securing digital communications, and compressing data have real-world implications that touch our daily lives. Moreover, in the realm of mathematics, prime factors are the bedrock upon which the understanding of integers and number theory is built. They continue to inspire, challenge, and enrich the world of mathematics and science. So, the next time you encounter a prime number or find yourself simplifying a fraction, remember that you’re tapping into the power of prime factors, a fundamental concept with an enduring impact on our modern world.
The Fundamental Theorem of Arithmetic

The Fundamental Theorem of Arithmetic, a cornerstone of number theory, is a deceptively simple yet profoundly powerful concept in the world of mathematics. This theorem states that every positive integer greater than 1 can be uniquely represented as a product of prime numbers. While this statement may seem straightforward, it carries immense significance and has far-reaching implications, particularly when it comes to the world of prime factors.
Explanation of the Theorem:
At its core, the Fundamental Theorem of Arithmetic tells us that every integer can be factored into a unique set of prime numbers. This uniqueness is what distinguishes prime factorization from other forms of factorization. For example, consider the number 12. It can be expressed as the product of its prime factors: 2 * 2 * 3. No matter how you arrange these prime factors, the result is always the same: 2 * 2 * 3. This uniqueness is what makes prime factorization an essential and powerful tool in mathematics.
How it Relates to Finding Prime Factors:
The relationship between the Fundamental Theorem of Arithmetic and finding prime factors is intrinsic. In fact, the theorem is the very foundation upon which prime factorization rests. Here’s how it all ties together:
Prime Factorization: The theorem serves as the theoretical basis for prime factorization. It tells us that every integer can be factored into a unique set of prime numbers, which are the building blocks of all numbers. This uniqueness is what allows us to break down any integer into its prime factors in a systematic and unambiguous way.
Simplifying Fractions: Prime factorization, stemming from the theorem, plays a pivotal role in simplifying fractions. When we find the prime factors of the numerator and denominator of a fraction, we can cancel out common factors, simplifying the fraction to its lowest terms. This simplification is a direct application of the Fundamental Theorem of Arithmetic and is indispensable in various fields, from everyday life to engineering and science.
Number Properties: Understanding the theorem also helps us gain insights into the properties of numbers. For example, we can easily determine whether a number is even or odd based on its prime factorization. If it has 2 as one of its prime factors, it’s even; otherwise, it’s odd. This simple rule is rooted in the theorem and is a testament to its practicality.
Cryptography: The security of online transactions and communications relies on the difficulty of factoring large semiprime numbers, which are products of two prime numbers. The Fundamental Theorem of Arithmetic, by ensuring unique prime factorization, underpins the security of encryption algorithms like RSA. Without the theorem’s assurance of prime factorization’s uniqueness, our digital world would be far less secure.
Method 1: Trial Division
Method 1: Trial Division – Unlocking Prime Factors Step by Step
In the captivating journey of understanding prime factors, one of the fundamental methods that stands out is Trial Division. This method, with its simplicity and effectiveness, serves as a valuable tool in the arsenal of mathematicians, students, and problem solvers alike. Let’s delve into a comprehensive step-by-step guide on how to use Trial Division to find prime factors, accompanied by illustrative examples to enhance clarity.
Step 1: Starting with the Basics Begin by selecting the number you want to find the prime factors of. For our example, let’s take the number 36.
Step 2: Identify the Potential Divisors To start the trial division process, you’ll need to identify potential divisors. These are the numbers that you’ll test to see if they evenly divide your target number. In this case, since we’re looking for prime factors, we’ll start with the smallest prime number, which is 2. So, our potential divisor is 2.
Step 3: Trial Division Now comes the trial division itself. Divide the target number (36) by the potential divisor (2). In this case, 36 ÷ 2 equals 18. If the division results in an integer quotient (no remainder), it means that 2 is a factor of 36.
Step 4: Record the Factor As we’ve successfully divided 36 by 2 without any remainder, we record 2 as a factor of 36. It’s important to remember that we’re not done yet; we continue with the process until we can no longer divide evenly.
Step 5: Proceeding with Prime Factors Next, we move on to the next potential divisor, which is also 2 in this case. Now, we divide 18 (the result from the previous division) by 2. The result is 9, which is an integer. So, we record another 2 as a factor.
Step 6: Continue the Process We repeat the process, dividing the new result (9) by 2. However, this time, we encounter a remainder. When we divide 9 by 2, we get 4 with a remainder of 1. This tells us that 2 is no longer a factor of 9.
Step 7: Move to the Next Prime At this point, we’ve exhausted all possibilities with the current divisor (2). So, we move on to the next prime number, which is 3. We divide 9 by 3, and it evenly divides, resulting in 3. We record 3 as a factor.
Step 8: Continue until Completion We continue with this process until we reach a point where the target number cannot be divided by any prime number without a remainder. In this example, we have successfully found all prime factors of 36: 2, 2, 3.
Illustrative Example: Prime Factors of 36 To illustrate this process further, let’s find the prime factors of 36 using Trial Division:
- Start with 36.
- Divide by 2: 36 ÷ 2 = 18. Record 2 as a factor.
- Divide by 2 again: 18 ÷ 2 = 9. Record another 2 as a factor.
- Divide by 2 once more: 9 ÷ 2 = 4 with a remainder of 1.
- Move on to the next prime, 3: 9 ÷ 3 = 3. Record 3 as a factor.
- Continue until no more prime divisions are possible.
In the end, we find that the prime factors of 36 are indeed 2, 2, and 3.
Trial Division, with its systematic approach, empowers us to break down complex numbers into their prime constituents, unraveling the mathematical secrets that underlie them. Whether you’re solving mathematical puzzles, simplifying fractions, or securing data through prime factorization algorithms, Trial Division is a valuable technique that enhances your problem-solving toolkit. So, as you embark on your journey to uncover prime factors, remember this method as your reliable guide, illuminating the path to mathematical understanding.
Method 2: Sieve of Eratosthenes
Method 2: Sieve of Eratosthenes – Unearthing Prime Factors with Ancient Wisdom
The Sieve of Eratosthenes, an ancient algorithm devised by the Greek mathematician Eratosthenes, stands as a timeless testament to human ingenuity in the quest to unearth prime numbers. Its elegance lies in its simplicity, offering an efficient way to not only identify prime numbers but also to find prime factors. In this exploration, we’ll embark on a journey to unravel the intricacies of this method, which has been a mathematical beacon for centuries.
Introduction to the Sieve of Eratosthenes:
The Sieve of Eratosthenes is a mathematical sieve that systematically sieves out composite numbers to reveal the prime numbers within a given range. Its origin dates back to approximately 240 BCE, making it one of the oldest known algorithms in history. Eratosthenes, a scholar of diverse talents, designed this method to address the fundamental question of identifying all prime numbers within a specified limit.
Detailed Instructions on Implementing the Sieve:
Implementing the Sieve of Eratosthenes to find prime factors involves a systematic and iterative process. Here’s a step-by-step guide:
Step 1: Set Up the Sieve
- Begin by creating a list of numbers from 2 to the maximum value you want to investigate for prime factors.
Step 2: Start with the First Prime
- Begin with the first number in the list, which is 2. Mark it as a prime number.
- Cross out all multiples of 2 in the list, as they are composite numbers.
- Move on to the next unmarked number in the list, which is 3. Mark it as a prime.
- Cross out all multiples of 3 that are still unmarked.
Step 3: Repeat and Iterate
- Continue this process, marking the next unmarked number as a prime and crossing out its multiples.
- Keep repeating until you have checked all numbers in the list.
Step 4: Collect Prime Numbers
- Once you’ve completed the process, the numbers that remain unmarked in the list are prime numbers.
- These prime numbers can be used to identify prime factors.
Using the Sieve to Find Prime Factors:
To find prime factors of a specific number using the Sieve of Eratosthenes, you can follow these steps:
Create a list of prime numbers generated using the Sieve within a suitable range (e.g., up to the square root of the target number).
Begin with the first prime number in your list and check if it divides the target number evenly.
If it does, record the prime factor and divide the target number by that prime factor.
Continue with the next prime number in your list and repeat the process until the target number becomes 1.
The prime factors you’ve recorded are the prime factors of the original number.
Illustrative Example: Finding Prime Factors of 36 To illustrate this method, let’s find the prime factors of 36 using the Sieve of Eratosthenes:
Generate a list of prime numbers up to the square root of 36: 2, 3.
Start with the first prime, 2. Check if 2 divides 36 evenly. It does (36 ÷ 2 = 18), so we record 2 as a prime factor and update 36 to 18.
Proceed with the next prime, 3. Check if 3 divides 18 evenly. It does (18 ÷ 3 = 6), so we record 3 as another prime factor and update 18 to 6.
Continue with the next prime, which is 3 again. Check if 3 divides 6 evenly. It does (6 ÷ 3 = 2), so we record 3 as a prime factor once more and update 6 to 2.
Finally, check if 3 divides 2 evenly. It doesn’t.
We have now completed the process, and the prime factors of 36 are 2 and 3.
The Sieve of Eratosthenes, with its historical significance and enduring utility, continues to be a valuable method for finding prime factors and prime numbers alike. Its elegance and efficiency have made it a cornerstone of number theory, offering a window into the world of prime factorization and mathematical exploration. So, as you navigate the realm of prime factors, consider the wisdom of Eratosthenes, whose ancient sieve still guides our mathematical discoveries today.
Method 3: Prime Factorization Algorithm
Method 3: Prime Factorization Algorithm – Mathematical Precision
The Prime Factorization Algorithm is a systematic approach to unraveling the prime factors of an integer. It starts with the smallest prime, divides the number, and continues until it can no longer divide evenly. Here’s a brief breakdown:
Begin with the Number: Start with the integer you want to factorize.
Smallest Prime (2): Check if it’s divisible by 2. If yes, divide and record.
Move to the Next Prime: Proceed to the next prime number and repeat the process until the number is 1.
Let’s illustrate this with 945:
- Start with 945.
- Divide by 3 (945 ÷ 3 = 315), record 3.
- Continue with 7 (315 ÷ 7 = 45), record 7.
The prime factors of 945 are 3 and 7. The algorithm’s efficiency shines when dealing with larger numbers, making it a powerful tool in mathematics.
Finding Prime Factors of Large Numbers
Finding Prime Factors of Large Numbers – Unlocking the Secrets of Cryptography
In the realm of mathematics, the pursuit of prime factors takes us on a captivating journey through numbers, revealing their fundamental building blocks. However, when dealing with large numbers, the quest becomes not just an intellectual challenge but also a critical component of fields like cryptography, where the security of sensitive information relies on the difficulty of factorization. In this exploration, we’ll delve into techniques and strategies for efficiently finding prime factors of large numbers, shedding light on their significance in the world of cryptography.
Techniques and Strategies for Efficiently Finding Prime Factors of Large Numbers:
Trial Division: This fundamental method involves dividing the number by smaller primes to check for divisibility. While effective for smaller numbers, it becomes impractical for extremely large ones due to the sheer number of potential divisors.
Pollard’s Rho Algorithm: A randomized algorithm, Pollard’s Rho, is a powerful tool for factorization. It employs a clever approach, simulating the behavior of a random walk in a cyclic group. Its efficiency and versatility make it a valuable choice for tackling large numbers.
Elliptic Curve Factorization: Leveraging the properties of elliptic curves, this method has gained popularity for its applicability in cryptography. It offers a robust and efficient approach to factorizing large semiprime numbers, which are the product of two prime numbers.
Number Field Sieve: The Number Field Sieve is the go-to algorithm for tackling the factorization of extremely large numbers. While it’s complex and resource-intensive, it’s capable of breaking down numbers that are several hundred digits long, making it essential for modern cryptography.
The Importance of Prime Factorization in Cryptography:
The significance of prime factorization in cryptography cannot be overstated. It forms the basis of many encryption algorithms, including RSA (Rivest–Shamir–Adleman), one of the most widely used encryption methods in secure communication. Here’s why prime factorization is pivotal:
RSA Encryption: RSA encryption relies on the difficulty of factoring the product of two large prime numbers. The public key, which is used for encryption, is derived from these two primes, while the private key, used for decryption, is generated by the knowledge of their factors. Breaking RSA encryption involves finding these prime factors, making factorization efforts a critical aspect of cryptographic security.
Cryptography Strength: The security of encrypted data hinges on the time and computational power required to factorize large numbers. The larger the prime factors, the more secure the encryption. As factorization techniques advance, encryption methods must evolve to use even larger prime numbers to maintain their strength against attacks.
Cryptographic Protocols: Beyond encryption, prime factorization plays a crucial role in various cryptographic protocols, such as digital signatures and key exchange. In these protocols, the difficulty of factorization ensures the authenticity and confidentiality of digital communication.
Secure Transactions: Prime factorization safeguards financial transactions, online communication, and sensitive data storage. It ensures that confidential information remains inaccessible to malicious actors.
Prime Factors and Fraction Simplification

Prime Factors and Fraction Simplification: Unlocking the Power of Primes
In the world of mathematics, the beauty often lies in its ability to simplify complex concepts and operations. Prime factors, those essential building blocks of integers, play a pivotal role not only in understanding numbers but also in simplifying fractions. In this exploration, we’ll uncover the remarkable connection between prime factorization and fraction simplification, with clear examples that demonstrate the elegant power of primes in making mathematics more accessible.
How Prime Factorization Helps Simplify Fractions:
Prime factorization, the process of breaking down an integer into its prime components, forms the foundation for simplifying fractions. It’s a fundamental concept that enables us to express fractions in their simplest, most reduced form. Here’s how it works:
Common Factors: When you have two integers, their common factors are essential in simplifying fractions. Prime factorization reveals the prime factors of both the numerator and the denominator.
Cancellation: By identifying the common prime factors, you can cancel them out from both the numerator and the denominator, reducing the fraction to its simplest form.
Provide Examples of Fraction Simplification Using Prime Factors:
Let’s illustrate the concept with a couple of examples:
Example 1: Simplifying 16/24
Prime Factorization:
- Numerator (16): 2 * 2 * 2 * 2
- Denominator (24): 2 * 2 * 2 * 3
Identify Common Factors:
- In this case, the common factor is 2, as both the numerator and denominator have four 2’s.
Cancel Common Factors:
- We can cancel out four 2’s from both the numerator and denominator, leaving us with 1/3.
Example 2: Simplifying 36/48
Prime Factorization:
- Numerator (36): 2 * 2 * 3 * 3
- Denominator (48): 2 * 2 * 2 * 2 * 3
Identify Common Factors:
- The common factors are 2 and 3, as both the numerator and denominator have these prime factors.
Cancel Common Factors:
- We can cancel out the common factors, leaving us with 3/4.
These examples demonstrate how prime factorization not only unveils the underlying structure of numbers but also simplifies fractions by revealing common factors that can be canceled out. This process not only aids in understanding fractions but also proves invaluable in various mathematical applications.
Common Pitfalls and Mistakes
Common Pitfalls and Mistakes in Prime Factorization: A Roadmap to Accuracy
Navigating the intricate terrain of prime factorization can be both a captivating journey and a perilous adventure. As we seek to uncover the building blocks of numbers, it’s important to be aware of the common pitfalls and mistakes that can lead us astray. In this guide, we’ll shine a light on these errors, offering valuable tips to avoid them and ensure accurate prime factorization.
Highlighting Common Errors People Make When Finding Prime Factors:
Incomplete Prime Factorization: One common mistake is stopping the factorization process too soon. This leaves numbers partially factored and can lead to incorrect results. For instance, in the factorization of 48, one might stop at 2 * 24, missing the prime factor of 3.
Ignoring Multiplicity: Prime factorization must consider the multiplicity of prime factors. Neglecting this aspect can result in overlooking repeated prime factors within a number. For instance, the prime factorization of 36 should include 2^2 * 3^2, acknowledging that 2 and 3 are repeated.
Misidentifying Prime Numbers: Some individuals mistakenly identify non-prime numbers as prime. It’s crucial to remember that prime numbers are divisible only by 1 and themselves. Incorrectly classifying a composite number as prime can lead to inaccurate factorization.
Skipping Small Prime Factors: Overlooking small prime factors like 2, 3, or 5 when dealing with larger numbers can be a significant error. These primes often play a critical role in the factorization process, simplifying the task.
Disregarding Negative Factors: In some cases, people forget to factor in negative prime factors when dealing with negative integers. Prime factorization applies to both positive and negative numbers, and ignoring this aspect can lead to errors.
Tips to Avoid These Mistakes:
Complete Factorization: Ensure that you continue the factorization process until you’ve reached a point where all factors are prime. This guarantees accuracy and completeness.
Multiplicity Matters: Pay attention to the exponent of prime factors, especially when they are repeated. Use superscripts to indicate multiplicity, ensuring no factors are overlooked.
Prime Number Recognition: Familiarize yourself with prime numbers and their properties. This will help you quickly identify whether a number is prime or composite.
Start Small: Begin the factorization process by identifying and factoring out the smallest prime factors. This often simplifies the task and reduces the chances of error.
Consider Negatives: Remember to apply prime factorization to negative integers as well, considering both the positive and negative prime factors.
Prime Factors in Real Life
Prime Factors in Real Life: Uncovering the Hidden Mathematics
In the tapestry of everyday life, mathematics often weaves its intricate patterns, even in places we may not immediately recognize. Prime factors, those fundamental building blocks of numbers, serve as an unassuming yet essential tool that quietly influences various aspects of our daily existence. Let’s delve into real-world scenarios where understanding prime factors can be not just advantageous but enlightening.
1. Cryptography and Data Security:
In the digital age, data security is paramount. Prime factors play a central role in encryption algorithms, particularly in the RSA algorithm. The security of online transactions, confidential messages, and sensitive data relies on the difficulty of factoring the product of two large prime numbers. Understanding prime factors in this context underscores the importance of safeguarding our digital lives.
2. Banking and Finance:
Prime factors also find their way into the financial sector. When you use an ATM or make online transactions, prime factorization algorithms ensure the security of your PIN or password. Prime-based encryption protects financial data from falling into the wrong hands, highlighting the real-world applications of these mathematical marvels.
3. Internet and Data Transfer:
In the realm of internet communication, prime numbers help facilitate secure data transfer. Protocols like SSL/TLS use prime factors to establish secure connections between web browsers and servers. This ensures that your personal information remains confidential when you shop online, pay bills, or access your bank accounts.
4. Factoring Large Numbers:
Outside the realm of cybersecurity, prime factors find applications in fields such as economics, where they are used to study economic cycles and predict market behavior. Mathematicians and economists use prime factorization to factorize large numbers, revealing insights into the underlying dynamics of complex systems.
5. Environmental Science:
Even environmental science benefits from prime factors. When analyzing population dynamics or studying ecological interactions, prime numbers can emerge as essential components in mathematical models. They help scientists predict the growth or decline of populations and understand the underlying patterns in ecosystems.
6. Music and Sound Engineering:
In the realm of sound engineering and music theory, prime factors influence the perception of harmony and discord. Musical intervals, such as the octave (2:1 frequency ratio), are based on simple prime number relationships. Understanding these prime factors allows musicians and engineers to create harmonious compositions and design audio equipment.
7. Factorization in Manufacturing:
Manufacturing processes often involve factorization for quality control and efficiency. For instance, in the production of printed circuit boards, understanding the prime factors of product dimensions can help optimize the layout, minimize waste, and reduce production costs.
8. Cryptocurrencies and Blockchain Technology:
In the world of cryptocurrencies like Bitcoin, prime factors are at the heart of cryptographic protocols. They ensure the security of digital wallets and transactions, fostering trust in decentralized financial systems.
9. Medical Research:
Even medical researchers employ prime factorization in the analysis of genetic data. Algorithms based on prime factors assist in deciphering complex genetic patterns and identifying disease markers, contributing to advancements in healthcare.
In summary, prime factors may seem like abstract mathematical concepts, but they possess real-world significance that touches various aspects of our lives. From securing our online transactions to shaping the harmony of music and influencing economic models, prime factors quietly shape the world around us. Recognizing their presence in these diverse domains highlights the profound and practical impact of mathematics on our daily existence, reaffirming that the hidden beauty of prime numbers extends far beyond the confines of mathematical theory.
Most asked questions
- How do prime factors relate to prime numbers?
Prime factors and prime numbers are intimately connected in mathematics. Prime numbers are the building blocks of all positive integers, and prime factorization is the process of breaking down a composite number into its prime constituents.
Every positive integer greater than 1 can be expressed as a unique product of prime numbers, known as its prime factorization. For example, the prime factorization of 12 is 2 × 2 × 3, where 2 and 3 are prime numbers. Prime factors are the prime numbers that divide a given number without leaving a remainder.
Prime numbers, by definition, have only two distinct positive divisors: 1 and themselves. Therefore, when a number’s prime factorization includes multiple prime numbers, it signifies that the number is not prime but composite. Conversely, if a number’s prime factorization contains only one prime number, it is itself a prime number.
In summary, prime factors are the prime numbers that compose a composite number, while prime numbers are those numbers that have exactly two distinct positive divisors, themselves and 1. Understanding the relationship between prime factors and prime numbers is fundamental in number theory and various mathematical applications.
- Can prime factors help in simplifying radicals?
Yes, prime factors play a crucial role in simplifying radicals. Radicals involve square roots, cube roots, or higher-order roots of numbers. When we seek to simplify a radical expression, we aim to find the simplest form with no perfect roots left under the radical symbol.
Prime factorization comes into play by breaking down the number inside the radical into its prime factors. For example, consider the square root of 72. By prime factorizing 72 into 2^3 * 3^2, we can simplify the radical as √(2^3 * 3^2). Then, using the property of radicals, we can rewrite this as 2^1 * 3^1 * √2, which is a simplified form.
In summary, prime factors provide the foundation for simplifying radicals by breaking down numbers into their basic prime components. This process allows us to express radical expressions in their simplest, most readable form, making mathematical calculations more manageable.
- What is the significance of prime factors in computer science?
Prime factors hold significant relevance in computer science, particularly in the fields of cryptography and algorithm design.
In cryptography, prime factors play a pivotal role in RSA encryption, one of the most widely used encryption methods for securing sensitive data online. The security of RSA encryption relies on the difficulty of factoring large composite numbers into their prime factors. This factorization process forms the foundation of RSA’s security, as breaking down a large number into its prime constituents is computationally intensive and time-consuming, making it extremely challenging for cybercriminals to decipher encrypted information.
Furthermore, prime factors are fundamental in algorithm design and analysis. They are used in various algorithms, such as those for searching, sorting, and optimizing. Prime numbers, for instance, are crucial in generating random numbers for cryptographic applications and in ensuring efficient data structures and algorithms.
In conclusion, prime factors are not only mathematically significant but also vital in computer science, contributing to the security of online transactions and the optimization of various computational processes.
- How can prime factorization be used in solving word problems?
Prime factorization is a powerful tool in solving word problems across various disciplines. In mathematics and science, it helps find the greatest common factor (GCF) and the least common multiple (LCM) of numbers, facilitating the simplification of fractions and the coordination of events in probability and statistics.
In finance, prime factorization assists in calculating compound interest and determining the principal and interest payments in loans or investments.
In real-life scenarios, such as packing boxes of different sizes or distributing resources evenly, prime factorization helps optimize space and resources by identifying common factors and multiples.
Additionally, in cryptography, it plays a critical role in ensuring secure data transmission by encrypting and decrypting messages using large prime numbers.
In summary, prime factorization is a versatile problem-solving tool applicable in mathematics, science, finance, logistics, and cybersecurity, making it a fundamental concept with wide-reaching practical implications.
- Are there online tools to assist in finding prime factors?
Yes, there are numerous online tools available to assist in finding prime factors. These tools are especially valuable for dealing with large numbers or complex calculations. Online prime factorization calculators, such as Wolfram Alpha, Factoring Calculator, and various web-based mathematical software, offer quick and accurate solutions. Users can input a number, and these tools will efficiently break it down into its prime constituents.
Additionally, programming languages like Python provide libraries and functions for prime factorization, enabling developers to create customized solutions for specific needs.
These online tools and resources are incredibly convenient for students, mathematicians, programmers, and anyone working with prime factors, making complex factorization tasks more accessible and efficient.
- What are the prime factors of well-known numbers like 100, 500, or 1000?
The prime factors of well-known numbers like 100, 500, or 1000 can be determined by breaking down these numbers into their constituent prime numbers.
For 100: The prime factors are 2 and 5, as 100 = 2^2 * 5^2.
For 500: The prime factors are 2 and 5, as 500 = 2^2 * 5^3.
For 1000: The prime factors are 2 and 5, as 1000 = 2^3 * 5^3.
These prime factorizations reveal that common factors for these numbers are 2 and 5. The exponents indicate how many times each prime number is multiplied together to form the original number. Prime factorization is a fundamental concept in mathematics and is essential for various applications, including simplifying fractions, finding greatest common divisors, and solving mathematical problems.
- How does prime factorization apply to cryptography?
Prime factorization plays a crucial role in cryptography, particularly in the field of encryption and security. One of the most widely used encryption algorithms, RSA (Rivest-Shamir-Adleman), relies heavily on the difficulty of factoring the product of two large prime numbers. Here’s how it works:
Key Generation: In RSA encryption, two large prime numbers are selected, and their product is computed to create the public key. Factoring this product back into its constituent primes is extremely challenging and time-consuming, even for modern computers.
Encryption: Messages are encrypted using the recipient’s public key, which includes the product of the two primes. Without knowing the prime factors, it is computationally infeasible for an unauthorized party to decrypt the message.
Decryption: Only the recipient, who possesses the private key (containing the prime factors), can efficiently decrypt the message.
The security of RSA encryption relies on the difficulty of prime factorization, making it a cornerstone of modern cryptographic systems and ensuring the confidentiality and integrity of sensitive data in various applications, including online banking, e-commerce, and secure communication.
- What is the connection between prime factors and the greatest common divisor (GCD)?
The connection between prime factors and the greatest common divisor (GCD) lies in the fundamental theorem of arithmetic. This theorem states that every positive integer can be uniquely expressed as a product of prime numbers. When you find the prime factors of two numbers, you can determine their GCD, which is the largest positive integer that divides both numbers without leaving a remainder.
Here’s how it works:
Prime Factorization: Find the prime factors of each number. For example, for numbers like 36 and 48, the prime factorization would be 2^2 * 3^2 and 2^4 * 3, respectively.
Identify Common Prime Factors: Compare the prime factors of both numbers. In this case, both numbers share the prime factors 2 and 3.
Calculate GCD: To find the GCD, take the lowest power of each common prime factor. In our example, it would be 2^2 * 3 = 12.
So, the GCD of 36 and 48 is 12. Prime factorization provides a systematic way to calculate the GCD of any two positive integers, making it a valuable tool in mathematics, number theory, and various problem-solving scenarios.
- Can you explain prime factors in the context of algebraic expressions?
Certainly! Prime factors play a crucial role in simplifying algebraic expressions. When dealing with algebraic expressions, you often encounter complex polynomials or equations. Prime factorization helps break down these expressions into their simplest form, making calculations and understanding relationships between variables much more manageable.
Here’s how prime factors are relevant in algebraic expressions:
Common Factors: Prime factors help identify common factors in algebraic expressions. These common factors can be simplified or factored out, reducing the complexity of the expression.
Simplification: Prime factorization simplifies expressions by canceling out common factors in both the numerator and denominator. This simplification aids in solving equations and finding solutions.
Factoring: Prime factors guide the factoring process, helping to express algebraic expressions as a product of simpler terms. This is particularly useful in solving quadratic equations or finding roots.
In algebra, prime factors are a fundamental tool for simplifying expressions, solving equations, and understanding the relationships between variables. They provide a systematic way to break down complex expressions into more manageable components, facilitating mathematical operations and problem-solving.
- How do I find the prime factors of a decimal number?
Finding the prime factors of a decimal number is a straightforward process. First, convert the decimal number to a fraction if it’s not already in that form. Then, follow these steps:
Reduce to Lowest Terms: Ensure the fraction is in its simplest form by reducing it to the lowest terms. This means finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it to simplify.
Prime Factorization: Once the fraction is in its simplest form, apply prime factorization separately to the numerator and denominator. Break down both into their prime factors.
Identify Common Factors: Compare the prime factors of the numerator and denominator to identify common factors. These are the prime factors shared by both.
Express as a Product: Write the simplified fraction as a product of its prime factors, using the common factors as canceling terms.
By following these steps, you can find the prime factors of a decimal number expressed as a fraction. This method ensures you work with whole numbers, making the prime factorization process more manageable.
I’m Dr Justin Boey, an Aesthetic Doctor in Singapore. I believe in open sharing of knowledge and skills to patients, blog readers and fellow doctors alike.











